
一个看似简单的电路只有两个器件,一个运算放大器和一个反馈电阻,通常用于将电流转换为电压。我们熟悉的光探测器或阻抗计电流检测放大器就是这样的电路。电路如图1所示,其中运算放大器的输入电容Ci显示在外面以方便分析。运算放大器的输入容抗通常约为Ci = 10pF。
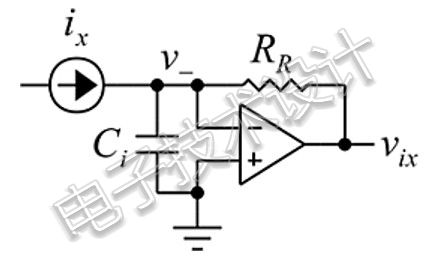
图1:一个看似简单的电路只有两个器件:运算放大器和反馈电阻。
这种电路可以在阻抗计中见到,通过被测器件(DUT)将未知电流ix转换为电压vix。仪器中的反馈电阻RR可在一定范围内调整,以覆盖较大范围DUT阻抗上的各种电流。
为了使电路尽量简单,我们选择了一个非常普通运算放大器——在fG处有一个主极点的电压反馈运算放大器。G是反馈环路的前向通路增益,H是反馈路径,这符合控制理论命名法。我们没有采用一般有源电路教科书中常见的A和β,而是用G和H,因为BJT对β的使用有严格要求。增益幅度随着频率的增加而降低,从高准静态(0+ Hz)增益G0降至fT处的增益1。运算放大器是反馈环路的前向通路,其电压增益为:
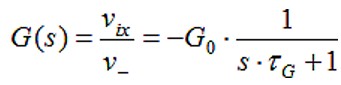
其中G0是开环运算放大器准静态增益幅度,fG=½xπxτG是开环带宽。在依赖于s的动态或频率相关因子G中,有时候使用极点或零时间常数(例如τG)而不是极点或零频率,公式计算更容易些。
这种运算放大器传递函数或增益有两种简化方式。第一种方式是高增益取近似值,使运算放大器更像是“运算式的”。将准静态增益G0近似为无穷大,或G0→∞,即可实现第一种运算放大器简化方式。将G的分子和分母除以1/G0,然后让G0接近无穷大,可以得到:
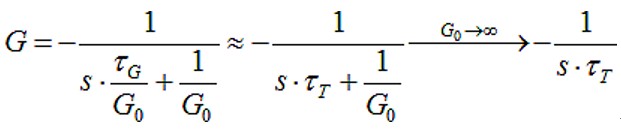
其中τT=1/2xπxfT=τG/G0。这就是无限G0、有限fT运算放大器的响应。图2是运算放大器的频响曲线,fbw(ol)是开环增益带宽,其开环增益的主极点沿开环増益曲线外沿而得到无限开环静态增益的原极点。开环增益为G,闭环增益包括反馈。
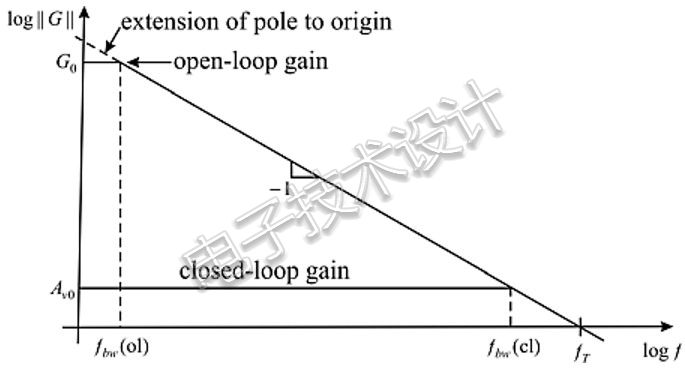
图2:具有开环带宽fbw(ol)的运算放大器的频率响应曲线图。
第二种运放简化方式是使其频率响应不受限制,这可通过让G的带宽变为无穷大来实现,这样就得到一个“无限快速”的运算放大器。随着τT降低(或fT增加),增益图向右(或向上)移动,即增益增加了。更快的放大器具有更大的准静态增益、更高的准静态环路增益GH0,以及更高的精度,但在具有慢极点的电路中可能不太稳定。具有无限G0和无限fT的运放是理想的运算放大器,也是常见的反相和同相增益公式中的运算放大器。
无限带宽的近似不如无限增益的近似那么实用,这种近似有时会产生振荡放大器。因此,为了理解看似简单的运算放大器电路,通常必须在增益变量中包含单极点,然后对放大器动态特性进行评估。除非慢速、高精度应用,否则运算放大器一般都采用无限G0,而不是无限fT。
闭环放大器是具有传递函数的互阻抗(电流输入,电压输出)放大器:
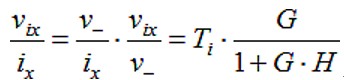
闭环反馈公式是理性因数,其中电压增益为vix/v–。Ti是反馈环路输入之前的ix-v–传递函数。它不在环路中,但却纠缠在一起。Ci与RR形成输入阻抗:
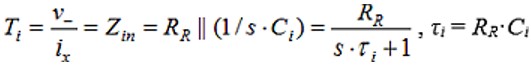
放大器的反馈部分是一个电压放大器,其输入v–=ixxZin。
因为在一个方向上的分压器可以是H,而在另一个方向上是Ti,所以一般反馈公式中总是包括Ti和To是一个好办法,因此:
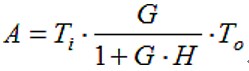
该反馈公式对应于图3所示的通用方框图,其中x可以是电压或电流。
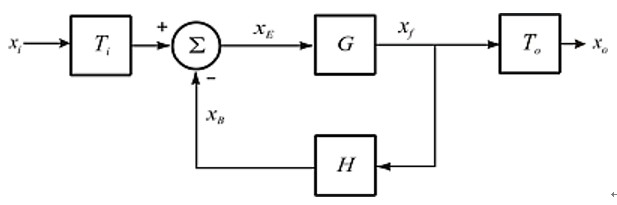
图3:反馈公式对应的通用方框图。
对于同相运算放大器配置,跟To一样,Ti=1。但是有一些电路(例如这种跨阻放大器),其环路中的电路元件可能会在环路前或环路后对增益产生影响,认识到这一点非常重要。
H是反馈路径传递函数,具有与Ti相同的Ci和RR,但作为输出到误差电压v-的分压器:
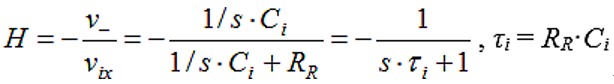
反馈误差求和(图3中带Σ的圆)是通过分压器和输入电压的叠加在电路中完成的:输入量ix通过Ti加给反馈量,得到输出H。闭环公式的反馈误差求和从反馈电压中减去输入电压,但由于分压器增加(不反转),H中的负号纠正了非反转,因此公式保持正确并且与方框图一致。
GH=GxH是环路增益,这是我们感兴趣的,因为它决定了环路稳定性。G、H和Ti,当被代入单极、无限G0运算放大器的反馈公式时,可以得到闭环互阻抗:
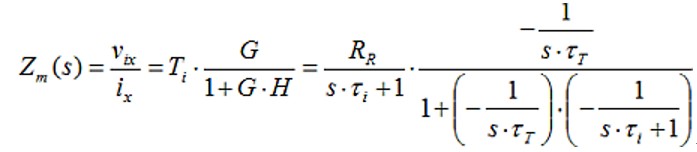
虽然RR是电阻,但跟频率相关的Ci和运算放大器使得闭环响应成为一个阻抗,因此公式简化为:
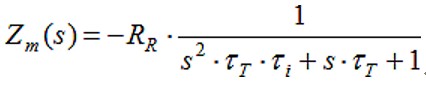
在s=0+Hz时,增益是反相跨阻抗–RR,与预期的一样。频率效应出现在分母的极点上。放大器具有双极(二次)响应,其中极点为:
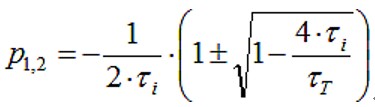
在第二部分“‘看似简单的电路:跨阻放大器’之跨阻放大器动态特性”中,我们将探讨Zm(s)电路特性带来的结果。
延伸阅读:“看似简单的电路:跨阻放大器”之跨阻放大器动态特性
(原文刊登于ASPENCORE旗下网站Planet Analog,参考链接:Seemingly Simple Circuits: Transresistance Amplifier, Part 1-- Approximating Op-Amps。)
《电子技术设计》2018年10月刊版权所有,禁止转载。
 最前沿的电子设计资讯
最前沿的电子设计资讯